\(
\newcommand{\A} {\mathbb{A}}
\newcommand{\rma} {\mathrm{a}}
\newcommand{\rmA} {\mathrm{A}}
\newcommand{\ba} {\mathbf{a}}
\newcommand{\bA} {\mathbf{A}}
\newcommand{\cA} {\mathcal{A}}
\newcommand{\bcA} {\boldsymbol{\cA}}
\newcommand{\tnsrA} {\underline{\bA}}
\newcommand{\wta} {\widetilde{a}}
\newcommand{\wtA} {\widetilde{A}}
\newcommand{\wtrma} {\widetilde{\rma}}
\newcommand{\wtrmA} {\widetilde{\rmA}}
\newcommand{\wtba} {\widetilde{\ba}}
\newcommand{\wtbA} {\widetilde{\bA}}
\newcommand{\wha} {\widehat{a}}
\newcommand{\whA} {\widehat{A}}
\newcommand{\whrma} {\widehat{\rma}}
\newcommand{\whrmA} {\widehat{\rmA}}
\newcommand{\whba} {\widehat{\ba}}
\newcommand{\whbA} {\widehat{\bA}}
\newcommand{\whcA} {\widehat{\cA}}
\newcommand{\whtnsrA} {\widehat{\tnsrA}}
\newcommand{\B} {\mathbb{B}}
\newcommand{\rmb} {\mathrm{b}}
\newcommand{\rmB} {\mathrm{B}}
\newcommand{\bb} {\mathbf{b}}
\newcommand{\bB} {\mathbf{B}}
\newcommand{\cB} {\mathcal{B}}
\newcommand{\bcB} {\boldsymbol{\cB}}
\newcommand{\tnsrB} {\underline{\bB}}
\newcommand{\wtb} {\widetilde{b}}
\newcommand{\wtB} {\widetilde{B}}
\newcommand{\wtrmb} {\widetilde{\rmb}}
\newcommand{\wtrmB} {\widetilde{\rmB}}
\newcommand{\wtbb} {\widetilde{\bb}}
\newcommand{\wtbB} {\widetilde{\bB}}
\newcommand{\whb} {\widehat{b}}
\newcommand{\whB} {\widehat{B}}
\newcommand{\whrmb} {\widehat{\rmb}}
\newcommand{\whrmB} {\widehat{\rmB}}
\newcommand{\whbb} {\widehat{\bb}}
\newcommand{\whbB} {\widehat{\bB}}
\newcommand{\whcB} {\widehat{\cB}}
\newcommand{\whtnsrB} {\widehat{\tnsrB}}
\newcommand{\C} {\mathbb{C}}
\newcommand{\rmc} {\mathrm{c}}
\newcommand{\rmC} {\mathrm{C}}
\newcommand{\bc} {\mathbf{c}}
\newcommand{\bC} {\mathbf{C}}
\newcommand{\cC} {\mathcal{C}}
\newcommand{\bcC} {\boldsymbol{\cC}}
\newcommand{\tnsrC} {\underline{\bC}}
\newcommand{\wtc} {\widetilde{c}}
\newcommand{\wtC} {\widetilde{C}}
\newcommand{\wtrmc} {\widetilde{\rmc}}
\newcommand{\wtrmC} {\widetilde{\rmC}}
\newcommand{\wtbc} {\widetilde{\bc}}
\newcommand{\wtbC} {\widetilde{\bC}}
\newcommand{\whc} {\widehat{c}}
\newcommand{\whC} {\widehat{C}}
\newcommand{\whrmc} {\widehat{\rmc}}
\newcommand{\whrmC} {\widehat{\rmC}}
\newcommand{\whbc} {\widehat{\bc}}
\newcommand{\whbC} {\widehat{\bC}}
\newcommand{\whcC} {\widehat{\cC}}
\newcommand{\whtnsrC} {\widehat{\tnsrC}}
\newcommand{\D} {\mathbb{D}}
\newcommand{\rmd} {\mathrm{d}}
\newcommand{\rmD} {\mathrm{D}}
\newcommand{\bd} {\mathbf{d}}
\newcommand{\bD} {\mathbf{D}}
\newcommand{\cD} {\mathcal{D}}
\newcommand{\bcD} {\boldsymbol{\cD}}
\newcommand{\tnsrD} {\underline{\bD}}
\newcommand{\wtd} {\widetilde{d}}
\newcommand{\wtD} {\widetilde{D}}
\newcommand{\wtrmd} {\widetilde{\rmd}}
\newcommand{\wtrmD} {\widetilde{\rmD}}
\newcommand{\wtbd} {\widetilde{\bd}}
\newcommand{\wtbD} {\widetilde{\bD}}
\newcommand{\whd} {\widehat{d}}
\newcommand{\whD} {\widehat{D}}
\newcommand{\whrmd} {\widehat{\rmd}}
\newcommand{\whrmD} {\widehat{\rmD}}
\newcommand{\whbd} {\widehat{\bd}}
\newcommand{\whbD} {\widehat{\bD}}
\newcommand{\whcD} {\widehat{\cD}}
\newcommand{\whtnsrD} {\widehat{\tnsrD}}
\newcommand{\E} {\mathbb{E}}
\newcommand{\rme} {\mathrm{e}}
\newcommand{\rmE} {\mathrm{E}}
\newcommand{\be} {\mathbf{e}}
\newcommand{\bE} {\mathbf{E}}
\newcommand{\cE} {\mathcal{E}}
\newcommand{\bcE} {\boldsymbol{\cE}}
\newcommand{\tnsrE} {\underline{\bE}}
\newcommand{\wte} {\widetilde{e}}
\newcommand{\wtE} {\widetilde{E}}
\newcommand{\wtrme} {\widetilde{\rme}}
\newcommand{\wtrmE} {\widetilde{\rmE}}
\newcommand{\wtbe} {\widetilde{\be}}
\newcommand{\wtbE} {\widetilde{\bE}}
\newcommand{\whe} {\widehat{e}}
\newcommand{\whE} {\widehat{E}}
\newcommand{\whrme} {\widehat{\rme}}
\newcommand{\whrmE} {\widehat{\rmE}}
\newcommand{\whbe} {\widehat{\be}}
\newcommand{\whbE} {\widehat{\bE}}
\newcommand{\whcE} {\widehat{\cE}}
\newcommand{\whtnsrE} {\widehat{\tnsrE}}
\newcommand{\F} {\mathbb{F}}
\newcommand{\rmf} {\mathrm{f}}
\newcommand{\rmF} {\mathrm{F}}
\newcommand{\bff} {\mathbf{f}}
\newcommand{\bF} {\mathbf{F}}
\newcommand{\cF} {\mathcal{F}}
\newcommand{\bcF} {\boldsymbol{\cF}}
\newcommand{\tnsrF} {\underline{\bF}}
\newcommand{\wtf} {\widetilde{f}}
\newcommand{\wtF} {\widetilde{F}}
\newcommand{\wtrmf} {\widetilde{\rmf}}
\newcommand{\wtrmF} {\widetilde{\rmF}}
\newcommand{\wtbf} {\widetilde{\bf}}
\newcommand{\wtbF} {\widetilde{\bF}}
\newcommand{\whf} {\widehat{f}}
\newcommand{\whF} {\widehat{F}}
\newcommand{\whrmf} {\widehat{\rmf}}
\newcommand{\whrmF} {\widehat{\rmF}}
\newcommand{\whbf} {\widehat{\bf}}
\newcommand{\whbF} {\widehat{\bF}}
\newcommand{\whcF} {\widehat{\cF}}
\newcommand{\whtnsrF} {\widehat{\tnsrF}}
\newcommand{\G} {\mathbb{G}}
\newcommand{\rmg} {\mathrm{g}}
\newcommand{\rmG} {\mathrm{G}}
\newcommand{\bg} {\mathbf{g}}
\newcommand{\bG} {\mathbf{G}}
\newcommand{\cG} {\mathcal{G}}
\newcommand{\bcG} {\boldsymbol{\cG}}
\newcommand{\tnsrG} {\underline{\bG}}
\newcommand{\wtg} {\widetilde{g}}
\newcommand{\wtG} {\widetilde{G}}
\newcommand{\wtrmg} {\widetilde{\rmg}}
\newcommand{\wtrmG} {\widetilde{\rmG}}
\newcommand{\wtbg} {\widetilde{\bg}}
\newcommand{\wtbG} {\widetilde{\bG}}
\newcommand{\whg} {\widehat{g}}
\newcommand{\whG} {\widehat{G}}
\newcommand{\whrmg} {\widehat{\rmg}}
\newcommand{\whrmG} {\widehat{\rmG}}
\newcommand{\whbg} {\widehat{\bg}}
\newcommand{\whbG} {\widehat{\bG}}
\newcommand{\whcG} {\widehat{\cG}}
\newcommand{\whtnsrG} {\widehat{\tnsrG}}
\newcommand{\bbH} {\mathbb{H}}
\newcommand{\rmh} {\mathrm{h}}
\newcommand{\rmH} {\mathrm{H}}
\newcommand{\bh} {\mathbf{h}}
\newcommand{\bH} {\mathbf{H}}
\newcommand{\cH} {\mathcal{H}}
\newcommand{\bcH} {\boldsymbol{\cH}}
\newcommand{\tnsrH} {\underline{\bH}}
\newcommand{\wth} {\widetilde{h}}
\newcommand{\wtH} {\widetilde{H}}
\newcommand{\wtrmh} {\widetilde{\rmh}}
\newcommand{\wtrmH} {\widetilde{\rmH}}
\newcommand{\wtbh} {\widetilde{\bh}}
\newcommand{\wtbH} {\widetilde{\bH}}
\newcommand{\whh} {\widehat{h}}
\newcommand{\whH} {\widehat{H}}
\newcommand{\whrmh} {\widehat{\rmh}}
\newcommand{\whrmH} {\widehat{\rmH}}
\newcommand{\whbh} {\widehat{\bh}}
\newcommand{\whbH} {\widehat{\bH}}
\newcommand{\whcH} {\widehat{\cH}}
\newcommand{\whtnsrH} {\widehat{\tnsrH}}
\newcommand{\I} {\mathbb{I}}
\newcommand{\rmi} {\mathrm{i}}
\newcommand{\rmI} {\mathrm{I}}
\newcommand{\bi} {\mathbf{i}}
\newcommand{\bI} {\mathbf{I}}
\newcommand{\cI} {\mathcal{I}}
\newcommand{\bcI} {\boldsymbol{\cI}}
\newcommand{\tnsrI} {\underline{\bI}}
\newcommand{\wti} {\widetilde{i}}
\newcommand{\wtI} {\widetilde{I}}
\newcommand{\wtrmi} {\widetilde{\rmi}}
\newcommand{\wtrmI} {\widetilde{\rmI}}
\newcommand{\wtbi} {\widetilde{\bi}}
\newcommand{\wtbI} {\widetilde{\bI}}
\newcommand{\whi} {\widehat{i}}
\newcommand{\whI} {\widehat{I}}
\newcommand{\whrmi} {\widehat{\rmi}}
\newcommand{\whrmI} {\widehat{\rmI}}
\newcommand{\whbi} {\widehat{\bi}}
\newcommand{\whbI} {\widehat{\bI}}
\newcommand{\whcI} {\widehat{\cI}}
\newcommand{\whtnsrI} {\widehat{\tnsrI}}
\newcommand{\J} {\mathbb{J}}
\newcommand{\rmj} {\mathrm{j}}
\newcommand{\rmJ} {\mathrm{J}}
\newcommand{\bj} {\mathbf{j}}
\newcommand{\bJ} {\mathbf{J}}
\newcommand{\cJ} {\mathcal{J}}
\newcommand{\bcJ} {\boldsymbol{\cJ}}
\newcommand{\tnsrJ} {\underline{\bJ}}
\newcommand{\wtj} {\widetilde{j}}
\newcommand{\wtJ} {\widetilde{J}}
\newcommand{\wtrmj} {\widetilde{\rmj}}
\newcommand{\wtrmJ} {\widetilde{\rmJ}}
\newcommand{\wtbj} {\widetilde{\bj}}
\newcommand{\wtbJ} {\widetilde{\bJ}}
\newcommand{\whj} {\widehat{j}}
\newcommand{\whJ} {\widehat{J}}
\newcommand{\whrmj} {\widehat{\rmj}}
\newcommand{\whrmJ} {\widehat{\rmJ}}
\newcommand{\whbj} {\widehat{\bj}}
\newcommand{\whbJ} {\widehat{\bJ}}
\newcommand{\whcJ} {\widehat{\cJ}}
\newcommand{\whtnsrJ} {\widehat{\tnsrJ}}
\newcommand{\K} {\mathbb{K}}
\newcommand{\rmk} {\mathrm{k}}
\newcommand{\rmK} {\mathrm{K}}
\newcommand{\bk} {\mathbf{k}}
\newcommand{\bK} {\mathbf{K}}
\newcommand{\cK} {\mathcal{K}}
\newcommand{\bcK} {\boldsymbol{\cK}}
\newcommand{\tnsrK} {\underline{\bK}}
\newcommand{\wtk} {\widetilde{k}}
\newcommand{\wtK} {\widetilde{K}}
\newcommand{\wtrmk} {\widetilde{\rmk}}
\newcommand{\wtrmK} {\widetilde{\rmK}}
\newcommand{\wtbk} {\widetilde{\bk}}
\newcommand{\wtbK} {\widetilde{\bK}}
\newcommand{\whk} {\widehat{k}}
\newcommand{\whK} {\widehat{K}}
\newcommand{\whrmk} {\widehat{\rmk}}
\newcommand{\whrmK} {\widehat{\rmK}}
\newcommand{\whbk} {\widehat{\bk}}
\newcommand{\whbK} {\widehat{\bK}}
\newcommand{\whcK} {\widehat{\cK}}
\newcommand{\whtnsrK} {\widehat{\tnsrK}}
\newcommand{\bbL} {\mathbb{L}}
\newcommand{\rml} {\mathrm{l}}
\newcommand{\rmL} {\mathrm{L}}
\newcommand{\bl} {\mathbf{l}}
\newcommand{\bL} {\mathbf{L}}
\newcommand{\cL} {\mathcal{L}}
\newcommand{\bcL} {\boldsymbol{\cL}}
\newcommand{\tnsrL} {\underline{\bL}}
\newcommand{\wtl} {\widetilde{l}}
\newcommand{\wtL} {\widetilde{L}}
\newcommand{\wtrml} {\widetilde{\rml}}
\newcommand{\wtrmL} {\widetilde{\rmL}}
\newcommand{\wtbl} {\widetilde{\bl}}
\newcommand{\wtbL} {\widetilde{\bL}}
\newcommand{\whl} {\widehat{l}}
\newcommand{\whL} {\widehat{L}}
\newcommand{\whrml} {\widehat{\rml}}
\newcommand{\whrmL} {\widehat{\rmL}}
\newcommand{\whbl} {\widehat{\bl}}
\newcommand{\whbL} {\widehat{\bL}}
\newcommand{\whcL} {\widehat{\cL}}
\newcommand{\whtnsrL} {\widehat{\tnsrL}}
\newcommand{\M} {\mathbb{M}}
\newcommand{\rmm} {\mathrm{m}}
\newcommand{\rmM} {\mathrm{M}}
\newcommand{\bm} {\mathbf{m}}
\newcommand{\bM} {\mathbf{M}}
\newcommand{\cM} {\mathcal{M}}
\newcommand{\bcM} {\boldsymbol{\cM}}
\newcommand{\tnsrM} {\underline{\bM}}
\newcommand{\wtm} {\widetilde{m}}
\newcommand{\wtM} {\widetilde{M}}
\newcommand{\wtrmm} {\widetilde{\rmm}}
\newcommand{\wtrmM} {\widetilde{\rmM}}
\newcommand{\wtbm} {\widetilde{\bm}}
\newcommand{\wtbM} {\widetilde{\bM}}
\newcommand{\whm} {\widehat{m}}
\newcommand{\whM} {\widehat{M}}
\newcommand{\whrmm} {\widehat{\rmm}}
\newcommand{\whrmM} {\widehat{\rmM}}
\newcommand{\whbm} {\widehat{\bm}}
\newcommand{\whbM} {\widehat{\bM}}
\newcommand{\whcM} {\widehat{\cM}}
\newcommand{\whtnsrM} {\widehat{\tnsrM}}
\newcommand{\N} {\mathbb{N}}
\newcommand{\rmn} {\mathrm{n}}
\newcommand{\rmN} {\mathrm{N}}
\newcommand{\bn} {\mathbf{n}}
\newcommand{\bN} {\mathbf{N}}
\newcommand{\cN} {\mathcal{N}}
\newcommand{\bcN} {\boldsymbol{\cN}}
\newcommand{\tnsrN} {\underline{\bN}}
\newcommand{\wtn} {\widetilde{n}}
\newcommand{\wtN} {\widetilde{N}}
\newcommand{\wtrmn} {\widetilde{\rmn}}
\newcommand{\wtrmN} {\widetilde{\rmN}}
\newcommand{\wtbn} {\widetilde{\bn}}
\newcommand{\wtbN} {\widetilde{\bN}}
\newcommand{\whn} {\widehat{n}}
\newcommand{\whN} {\widehat{N}}
\newcommand{\whrmn} {\widehat{\rmn}}
\newcommand{\whrmN} {\widehat{\rmN}}
\newcommand{\whbn} {\widehat{\bn}}
\newcommand{\whbN} {\widehat{\bN}}
\newcommand{\whcN} {\widehat{\cN}}
\newcommand{\whtnsrN} {\widehat{\tnsrN}}
\newcommand{\bbO} {\mathbb{O}}
\newcommand{\rmo} {\mathrm{o}}
\newcommand{\rmO} {\mathrm{O}}
\newcommand{\bo} {\mathbf{o}}
\newcommand{\bO} {\mathbf{O}}
\newcommand{\cO} {\mathcal{O}}
\newcommand{\bcO} {\boldsymbol{\cO}}
\newcommand{\tnsrO} {\underline{\bO}}
\newcommand{\wto} {\widetilde{o}}
\newcommand{\wtO} {\widetilde{O}}
\newcommand{\wtrmo} {\widetilde{\rmo}}
\newcommand{\wtrmO} {\widetilde{\rmO}}
\newcommand{\wtbo} {\widetilde{\bo}}
\newcommand{\wtbO} {\widetilde{\bO}}
\newcommand{\who} {\widehat{o}}
\newcommand{\whO} {\widehat{O}}
\newcommand{\whrmo} {\widehat{\rmo}}
\newcommand{\whrmO} {\widehat{\rmO}}
\newcommand{\whbo} {\widehat{\bo}}
\newcommand{\whbO} {\widehat{\bO}}
\newcommand{\whcO} {\widehat{\cO}}
\newcommand{\whtnsrO} {\widehat{\tnsrO}}
\newcommand{\bbP} {\mathbb{P}}
\newcommand{\rmp} {\mathrm{p}}
\newcommand{\rmP} {\mathrm{P}}
\newcommand{\bp} {\mathbf{p}}
\newcommand{\bP} {\mathbf{P}}
\newcommand{\cP} {\mathcal{P}}
\newcommand{\bcP} {\boldsymbol{\cP}}
\newcommand{\tnsrP} {\underline{\bP}}
\newcommand{\wtp} {\widetilde{p}}
\newcommand{\wtP} {\widetilde{P}}
\newcommand{\wtrmp} {\widetilde{\rmp}}
\newcommand{\wtrmP} {\widetilde{\rmP}}
\newcommand{\wtbp} {\widetilde{\bp}}
\newcommand{\wtbP} {\widetilde{\bP}}
\newcommand{\whp} {\widehat{p}}
\newcommand{\whP} {\widehat{P}}
\newcommand{\whrmp} {\widehat{\rmp}}
\newcommand{\whrmP} {\widehat{\rmP}}
\newcommand{\whbp} {\widehat{\bp}}
\newcommand{\whbP} {\widehat{\bP}}
\newcommand{\whcP} {\widehat{\cP}}
\newcommand{\whtnsrP} {\widehat{\tnsrP}}
\newcommand{\Q} {\mathbb{Q}}
\newcommand{\rmq} {\mathrm{q}}
\newcommand{\rmQ} {\mathrm{Q}}
\newcommand{\bq} {\mathbf{q}}
\newcommand{\bQ} {\mathbf{Q}}
\newcommand{\cQ} {\mathcal{Q}}
\newcommand{\bcQ} {\boldsymbol{\cQ}}
\newcommand{\tnsrQ} {\underline{\bQ}}
\newcommand{\wtq} {\widetilde{q}}
\newcommand{\wtQ} {\widetilde{Q}}
\newcommand{\wtrmq} {\widetilde{\rmq}}
\newcommand{\wtrmQ} {\widetilde{\rmQ}}
\newcommand{\wtbq} {\widetilde{\bq}}
\newcommand{\wtbQ} {\widetilde{\bQ}}
\newcommand{\whq} {\widehat{q}}
\newcommand{\whQ} {\widehat{Q}}
\newcommand{\whrmq} {\widehat{\rmq}}
\newcommand{\whrmQ} {\widehat{\rmQ}}
\newcommand{\whbq} {\widehat{\bq}}
\newcommand{\whbQ} {\widehat{\bQ}}
\newcommand{\whcQ} {\widehat{\cQ}}
\newcommand{\whtnsrQ} {\widehat{\tnsrQ}}
\newcommand{\R} {\mathbb{R}}
\newcommand{\rmr} {\mathrm{r}}
\newcommand{\rmR} {\mathrm{R}}
\newcommand{\br} {\mathbf{r}}
\newcommand{\bR} {\mathbf{R}}
\newcommand{\cR} {\mathcal{R}}
\newcommand{\bcR} {\boldsymbol{\cR}}
\newcommand{\tnsrR} {\underline{\bR}}
\newcommand{\wtr} {\widetilde{r}}
\newcommand{\wtR} {\widetilde{R}}
\newcommand{\wtrmr} {\widetilde{\rmr}}
\newcommand{\wtrmR} {\widetilde{\rmR}}
\newcommand{\wtbr} {\widetilde{\br}}
\newcommand{\wtbR} {\widetilde{\bR}}
\newcommand{\whr} {\widehat{r}}
\newcommand{\whR} {\widehat{R}}
\newcommand{\whrmr} {\widehat{\rmr}}
\newcommand{\whrmR} {\widehat{\rmR}}
\newcommand{\whbr} {\widehat{\br}}
\newcommand{\whbR} {\widehat{\bR}}
\newcommand{\whcR} {\widehat{\cR}}
\newcommand{\whtnsrR} {\widehat{\tnsrR}}
\newcommand{\bbS} {\mathbb{S}}
\newcommand{\rms} {\mathrm{s}}
\newcommand{\rmS} {\mathrm{S}}
\newcommand{\bs} {\mathbf{s}}
\newcommand{\bS} {\mathbf{S}}
\newcommand{\cS} {\mathcal{S}}
\newcommand{\bcS} {\boldsymbol{\cS}}
\newcommand{\tnsrS} {\underline{\bS}}
\newcommand{\wts} {\widetilde{s}}
\newcommand{\wtS} {\widetilde{S}}
\newcommand{\wtrms} {\widetilde{\rms}}
\newcommand{\wtrmS} {\widetilde{\rmS}}
\newcommand{\wtbs} {\widetilde{\bs}}
\newcommand{\wtbS} {\widetilde{\bS}}
\newcommand{\whs} {\widehat{s}}
\newcommand{\whS} {\widehat{S}}
\newcommand{\whrms} {\widehat{\rms}}
\newcommand{\whrmS} {\widehat{\rmS}}
\newcommand{\whbs} {\widehat{\bs}}
\newcommand{\whbS} {\widehat{\bS}}
\newcommand{\whcS} {\widehat{\cS}}
\newcommand{\whtnsrS} {\widehat{\tnsrS}}
\newcommand{\T} {\mathbb{T}}
\newcommand{\rmt} {\mathrm{t}}
\newcommand{\rmT} {\mathrm{T}}
\newcommand{\bt} {\mathbf{t}}
\newcommand{\bT} {\mathbf{T}}
\newcommand{\cT} {\mathcal{T}}
\newcommand{\bcT} {\boldsymbol{\cT}}
\newcommand{\tnsrT} {\underline{\bT}}
\newcommand{\wtt} {\widetilde{t}}
\newcommand{\wtT} {\widetilde{T}}
\newcommand{\wtrmt} {\widetilde{\rmt}}
\newcommand{\wtrmT} {\widetilde{\rmT}}
\newcommand{\wtbt} {\widetilde{\bt}}
\newcommand{\wtbT} {\widetilde{\bT}}
\newcommand{\wht} {\widehat{t}}
\newcommand{\whT} {\widehat{T}}
\newcommand{\whrmt} {\widehat{\rmt}}
\newcommand{\whrmT} {\widehat{\rmT}}
\newcommand{\whbt} {\widehat{\bt}}
\newcommand{\whbT} {\widehat{\bT}}
\newcommand{\whcT} {\widehat{\cT}}
\newcommand{\whtnsrT} {\widehat{\tnsrT}}
\newcommand{\U} {\mathbb{U}}
\newcommand{\rmu} {\mathrm{u}}
\newcommand{\rmU} {\mathrm{U}}
\newcommand{\bu} {\mathbf{u}}
\newcommand{\bU} {\mathbf{U}}
\newcommand{\cU} {\mathcal{U}}
\newcommand{\bcU} {\boldsymbol{\cU}}
\newcommand{\tnsrU} {\underline{\bU}}
\newcommand{\wtu} {\widetilde{u}}
\newcommand{\wtU} {\widetilde{U}}
\newcommand{\wtrmu} {\widetilde{\rmu}}
\newcommand{\wtrmU} {\widetilde{\rmU}}
\newcommand{\wtbu} {\widetilde{\bu}}
\newcommand{\wtbU} {\widetilde{\bU}}
\newcommand{\whu} {\widehat{u}}
\newcommand{\whU} {\widehat{U}}
\newcommand{\whrmu} {\widehat{\rmu}}
\newcommand{\whrmU} {\widehat{\rmU}}
\newcommand{\whbu} {\widehat{\bu}}
\newcommand{\whbU} {\widehat{\bU}}
\newcommand{\whcU} {\widehat{\cU}}
\newcommand{\whtnsrU} {\widehat{\tnsrU}}
\newcommand{\V} {\mathbb{V}}
\newcommand{\rmv} {\mathrm{v}}
\newcommand{\rmV} {\mathrm{V}}
\newcommand{\bv} {\mathbf{v}}
\newcommand{\bV} {\mathbf{V}}
\newcommand{\cV} {\mathcal{V}}
\newcommand{\bcV} {\boldsymbol{\cV}}
\newcommand{\tnsrV} {\underline{\bV}}
\newcommand{\wtv} {\widetilde{v}}
\newcommand{\wtV} {\widetilde{V}}
\newcommand{\wtrmv} {\widetilde{\rmv}}
\newcommand{\wtrmV} {\widetilde{\rmV}}
\newcommand{\wtbv} {\widetilde{\bv}}
\newcommand{\wtbV} {\widetilde{\bV}}
\newcommand{\whv} {\widehat{v}}
\newcommand{\whV} {\widehat{V}}
\newcommand{\whrmv} {\widehat{\rmv}}
\newcommand{\whrmV} {\widehat{\rmV}}
\newcommand{\whbv} {\widehat{\bv}}
\newcommand{\whbV} {\widehat{\bV}}
\newcommand{\whcV} {\widehat{\cV}}
\newcommand{\whtnsrV} {\widehat{\tnsrV}}
\newcommand{\W} {\mathbb{W}}
\newcommand{\rmw} {\mathrm{w}}
\newcommand{\rmW} {\mathrm{W}}
\newcommand{\bw} {\mathbf{w}}
\newcommand{\bW} {\mathbf{W}}
\newcommand{\cW} {\mathcal{W}}
\newcommand{\bcW} {\boldsymbol{\cW}}
\newcommand{\tnsrW} {\underline{\bW}}
\newcommand{\wtw} {\widetilde{w}}
\newcommand{\wtW} {\widetilde{W}}
\newcommand{\wtrmw} {\widetilde{\rmw}}
\newcommand{\wtrmW} {\widetilde{\rmW}}
\newcommand{\wtbw} {\widetilde{\bw}}
\newcommand{\wtbW} {\widetilde{\bW}}
\newcommand{\whw} {\widehat{w}}
\newcommand{\whW} {\widehat{W}}
\newcommand{\whrmw} {\widehat{\rmw}}
\newcommand{\whrmW} {\widehat{\rmW}}
\newcommand{\whbw} {\widehat{\bw}}
\newcommand{\whbW} {\widehat{\bW}}
\newcommand{\whcW} {\widehat{\cW}}
\newcommand{\whtnsrW} {\widehat{\tnsrW}}
\newcommand{\X} {\mathbb{X}}
\newcommand{\rmx} {\mathrm{x}}
\newcommand{\rmX} {\mathrm{X}}
\newcommand{\bx} {\mathbf{x}}
\newcommand{\bX} {\mathbf{X}}
\newcommand{\cX} {\mathcal{X}}
\newcommand{\bcX} {\boldsymbol{\cX}}
\newcommand{\tnsrX} {\underline{\bX}}
\newcommand{\wtx} {\widetilde{x}}
\newcommand{\wtX} {\widetilde{X}}
\newcommand{\wtrmx} {\widetilde{\rmx}}
\newcommand{\wtrmX} {\widetilde{\rmX}}
\newcommand{\wtbx} {\widetilde{\bx}}
\newcommand{\wtbX} {\widetilde{\bX}}
\newcommand{\whx} {\widehat{x}}
\newcommand{\whX} {\widehat{X}}
\newcommand{\whrmx} {\widehat{\rmx}}
\newcommand{\whrmX} {\widehat{\rmX}}
\newcommand{\whbx} {\widehat{\bx}}
\newcommand{\whbX} {\widehat{\bX}}
\newcommand{\whcX} {\widehat{\cX}}
\newcommand{\whtnsrX} {\widehat{\tnsrX}}
\newcommand{\Y} {\mathbb{Y}}
\newcommand{\rmy} {\mathrm{y}}
\newcommand{\rmY} {\mathrm{Y}}
\newcommand{\by} {\mathbf{y}}
\newcommand{\bY} {\mathbf{Y}}
\newcommand{\cY} {\mathcal{Y}}
\newcommand{\bcY} {\boldsymbol{\cY}}
\newcommand{\tnsrY} {\underline{\bY}}
\newcommand{\wty} {\widetilde{y}}
\newcommand{\wtY} {\widetilde{Y}}
\newcommand{\wtrmy} {\widetilde{\rmy}}
\newcommand{\wtrmY} {\widetilde{\rmY}}
\newcommand{\wtby} {\widetilde{\by}}
\newcommand{\wtbY} {\widetilde{\bY}}
\newcommand{\why} {\widehat{y}}
\newcommand{\whY} {\widehat{Y}}
\newcommand{\whrmy} {\widehat{\rmy}}
\newcommand{\whrmY} {\widehat{\rmY}}
\newcommand{\whby} {\widehat{\by}}
\newcommand{\whbY} {\widehat{\bY}}
\newcommand{\whcY} {\widehat{\cY}}
\newcommand{\whtnsrY} {\widehat{\tnsrY}}
\newcommand{\Z} {\mathbb{Z}}
\newcommand{\rmz} {\mathrm{z}}
\newcommand{\rmZ} {\mathrm{Z}}
\newcommand{\bz} {\mathbf{z}}
\newcommand{\bZ} {\mathbf{Z}}
\newcommand{\cZ} {\mathcal{Z}}
\newcommand{\bcZ} {\boldsymbol{\cZ}}
\newcommand{\tnsrZ} {\underline{\bZ}}
\newcommand{\wtz} {\widetilde{z}}
\newcommand{\wtZ} {\widetilde{Z}}
\newcommand{\wtrmz} {\widetilde{\rmz}}
\newcommand{\wtrmZ} {\widetilde{\rmZ}}
\newcommand{\wtbz} {\widetilde{\bz}}
\newcommand{\wtbZ} {\widetilde{\bZ}}
\newcommand{\whz} {\widehat{z}}
\newcommand{\whZ} {\widehat{Z}}
\newcommand{\whrmz} {\widehat{\rmz}}
\newcommand{\whrmZ} {\widehat{\rmZ}}
\newcommand{\whbz} {\widehat{\bz}}
\newcommand{\whbZ} {\widehat{\bZ}}
\newcommand{\whcZ} {\widehat{\cZ}}
\newcommand{\whtnsrZ} {\widehat{\tnsrZ}}
\newcommand{\balpha} {\boldsymbol{\alpha}}
\newcommand{\wtalpha} {\widetilde{\alpha}}
\newcommand{\whalpha} {\widehat{\alpha}}
\newcommand{\wtbalpha} {\widetilde{\balpha}}
\newcommand{\whbalpha} {\widehat{\balpha}}
\newcommand{\bbeta} {\boldsymbol{\beta}}
\newcommand{\wtbeta} {\widetilde{\beta}}
\newcommand{\whbeta} {\widehat{\beta}}
\newcommand{\wtbbeta} {\widetilde{\bbeta}}
\newcommand{\whbbeta} {\widehat{\bbeta}}
\newcommand{\bgamma} {\boldsymbol{\gamma}}
\newcommand{\wtgamma} {\widetilde{\gamma}}
\newcommand{\whgamma} {\widehat{\gamma}}
\newcommand{\wtbgamma} {\widetilde{\bgamma}}
\newcommand{\whbgamma} {\widehat{\bgamma}}
\newcommand{\bdelta} {\boldsymbol{\delta}}
\newcommand{\wtdelta} {\widetilde{\delta}}
\newcommand{\whdelta} {\widehat{\delta}}
\newcommand{\wtbdelta} {\widetilde{\bdelta}}
\newcommand{\whbdelta} {\widehat{\bdelta}}
\newcommand{\bepsilon} {\boldsymbol{\epsilon}}
\newcommand{\wtepsilon} {\widetilde{\epsilon}}
\newcommand{\whepsilon} {\widehat{\epsilon}}
\newcommand{\wtbepsilon}{\widetilde{\bepsilon}}
\newcommand{\whbepsilon}{\widehat{\bepsilon}}
\newcommand{\veps} {\varepsilon}
\newcommand{\bveps} {\boldsymbol{\veps}}
\newcommand{\wtveps} {\widetilde{\veps}}
\newcommand{\whveps} {\widehat{\veps}}
\newcommand{\wtbveps} {\widetilde{\bveps}}
\newcommand{\whbveps} {\widehat{\bveps}}
\newcommand{\bEta} {\boldsymbol{\eta}}
\newcommand{\wteta} {\widetilde{\eta}}
\newcommand{\wheta} {\widehat{\eta}}
\newcommand{\wtbEta} {\widetilde{\bEta}}
\newcommand{\whbEta} {\widehat{\bEta}}
\newcommand{\btheta} {\boldsymbol{\theta}}
\newcommand{\wttheta} {\widetilde{\theta}}
\newcommand{\whtheta} {\widehat{\theta}}
\newcommand{\wtbtheta} {\widetilde{\btheta}}
\newcommand{\whbtheta} {\widehat{\btheta}}
\newcommand{\bvtheta} {\boldsymbol{\vartheta}}
\newcommand{\wtvtheta} {\widetilde{\vartheta}}
\newcommand{\whvtheta} {\widehat{\vartheta}}
\newcommand{\wtbvtheta} {\widetilde{\bvtheta}}
\newcommand{\whbvtheta} {\widehat{\bvtheta}}
\newcommand{\biota} {\boldsymbol{\iota}}
\newcommand{\wtiota} {\widetilde{\iota}}
\newcommand{\whiota} {\widehat{\iota}}
\newcommand{\wtbiota} {\widetilde{\biota}}
\newcommand{\whbiota} {\widehat{\biota}}
\newcommand{\bkappa} {\boldsymbol{\kappa}}
\newcommand{\wtkappa} {\widetilde{\kappa}}
\newcommand{\whkappa} {\widehat{\kappa}}
\newcommand{\wtbkappa} {\widetilde{\bkappa}}
\newcommand{\whbkappa} {\widehat{\bkappa}}
\newcommand{\blambda} {\boldsymbol{\lambda}}
\newcommand{\wtlambda} {\widetilde{\lambda}}
\newcommand{\whlambda} {\widehat{\lambda}}
\newcommand{\wtblambda} {\widetilde{\blambda}}
\newcommand{\whblambda} {\widehat{\blambda}}
\newcommand{\bmu} {\boldsymbol{\mu}}
\newcommand{\wtmu} {\widetilde{\mu}}
\newcommand{\whmu} {\widehat{\mu}}
\newcommand{\wtbmu} {\widetilde{\bmu}}
\newcommand{\whbmu} {\widehat{\bmu}}
\newcommand{\bnu} {\boldsymbol{\nu}}
\newcommand{\wtnu} {\widetilde{\nu}}
\newcommand{\whnu} {\widehat{\nu}}
\newcommand{\wtbnu} {\widetilde{\bnu}}
\newcommand{\whbnu} {\widehat{\bnu}}
\newcommand{\bxi} {\boldsymbol{\xi}}
\newcommand{\wtxi} {\widetilde{\xi}}
\newcommand{\whxi} {\widehat{\xi}}
\newcommand{\wtbxi} {\widetilde{\bxi}}
\newcommand{\whbxi} {\widehat{\bxi}}
\newcommand{\bpi} {\boldsymbol{\pi}}
\newcommand{\wtpi} {\widetilde{\pi}}
\newcommand{\whpi} {\widehat{\pi}}
\newcommand{\wtbpi} {\widetilde{\bpi}}
\newcommand{\whbpi} {\widehat{\bpi}}
\newcommand{\bvpi} {\boldsymbol{\varpi}}
\newcommand{\wtvpi} {\widetilde{\varpi}}
\newcommand{\whvpi} {\widehat{\varpi}}
\newcommand{\wtbvpi} {\widetilde{\bvpi}}
\newcommand{\whbvpi} {\widehat{\bvpi}}
\newcommand{\brho} {\boldsymbol{\rho}}
\newcommand{\wtrho} {\widetilde{\rho}}
\newcommand{\whrho} {\widehat{\rho}}
\newcommand{\wtbrho} {\widetilde{\brho}}
\newcommand{\whbrho} {\widehat{\brho}}
\newcommand{\bvrho} {\boldsymbol{\varrho}}
\newcommand{\wtvrho} {\widetilde{\varrho}}
\newcommand{\whvrho} {\widehat{\varrho}}
\newcommand{\wtbvrho} {\widetilde{\bvrho}}
\newcommand{\whbvrho} {\widehat{\bvrho}}
\newcommand{\bsigma} {\boldsymbol{\sigma}}
\newcommand{\wtsigma} {\widetilde{\sigma}}
\newcommand{\whsigma} {\widehat{\sigma}}
\newcommand{\wtbsigma} {\widetilde{\bsigma}}
\newcommand{\whbsigma} {\widehat{\bsigma}}
\newcommand{\bvsigma} {\boldsymbol{\varsigma}}
\newcommand{\wtvsigma} {\widetilde{\varsigma}}
\newcommand{\whvsigma} {\widehat{\varsigma}}
\newcommand{\wtbvsigma} {\widetilde{\bvsigma}}
\newcommand{\whbvsigma} {\widehat{\bvsigma}}
\newcommand{\btau} {\boldsymbol{\tau}}
\newcommand{\wttau} {\widetilde{\tau}}
\newcommand{\whtau} {\widehat{\tau}}
\newcommand{\wtbtau} {\widetilde{\btau}}
\newcommand{\whbtau} {\widehat{\btau}}
\newcommand{\bupsilon} {\boldsymbol{\upsilon}}
\newcommand{\wtupsilon} {\widetilde{\upsilon}}
\newcommand{\whupsilon} {\widehat{\upsilon}}
\newcommand{\wtbupsilon}{\widetilde{\bupsilon}}
\newcommand{\whbupsilon}{\widehat{\bupsilon}}
\newcommand{\bzeta} {\boldsymbol{\zeta}}
\newcommand{\wtzeta} {\widetilde{\zeta}}
\newcommand{\whzeta} {\widehat{\zeta}}
\newcommand{\wtbzeta}{\widetilde{\bzeta}}
\newcommand{\whbzeta}{\widehat{\bzeta}}
\newcommand{\bphi} {\boldsymbol{\phi}}
\newcommand{\wtphi} {\widetilde{\phi}}
\newcommand{\whphi} {\widehat{\phi}}
\newcommand{\wtbphi} {\widetilde{\bphi}}
\newcommand{\whbphi} {\widehat{\bphi}}
\newcommand{\bvphi} {\boldsymbol{\varphi}}
\newcommand{\wtvphi} {\widetilde{\varphi}}
\newcommand{\whvphi} {\widehat{\varphi}}
\newcommand{\wtbvphi} {\widetilde{\bvphi}}
\newcommand{\whbvphi} {\widehat{\bvphi}}
\newcommand{\bchi} {\boldsymbol{\chi}}
\newcommand{\wtchi} {\widetilde{\chi}}
\newcommand{\whchi} {\widehat{\chi}}
\newcommand{\wtbchi} {\widetilde{\bchi}}
\newcommand{\whbchi} {\widehat{\bchi}}
\newcommand{\bpsi} {\boldsymbol{\psi}}
\newcommand{\wtpsi} {\widetilde{\psi}}
\newcommand{\whpsi} {\widehat{\psi}}
\newcommand{\wtbpsi} {\widetilde{\bpsi}}
\newcommand{\whbpsi} {\widehat{\bpsi}}
\newcommand{\bomega} {\boldsymbol{\omega}}
\newcommand{\wtomega} {\widetilde{\omega}}
\newcommand{\whomega} {\widehat{\omega}}
\newcommand{\wtbomega} {\widetilde{\bomega}}
\newcommand{\whbomega} {\widehat{\bomega}}
\newcommand{\bGamma} {\boldsymbol{\Gamma}}
\newcommand{\wtGamma} {\widetilde{\Gamma}}
\newcommand{\whGamma} {\widehat{\Gamma}}
\newcommand{\wtbGamma} {\widetilde{\bGamma}}
\newcommand{\whbGamma} {\widehat{\bGamma}}
\newcommand{\bDelta} {\boldsymbol{\Delta}}
\newcommand{\wtDelta} {\widetilde{\Delta}}
\newcommand{\whDelta} {\widehat{\Delta}}
\newcommand{\wtbDelta} {\widetilde{\bDelta}}
\newcommand{\whbDelta} {\widehat{\bDelta}}
\newcommand{\bLambda} {\boldsymbol{\Lambda}}
\newcommand{\wtLambda} {\widetilde{\Lambda}}
\newcommand{\whLambda} {\widehat{\Lambda}}
\newcommand{\wtbLambda} {\widetilde{\bLambda}}
\newcommand{\whbLambda} {\widehat{\bLambda}}
\newcommand{\bXi} {\boldsymbol{\Xi}}
\newcommand{\wtXi} {\widetilde{\Xi}}
\newcommand{\whXi} {\widehat{\Xi}}
\newcommand{\wtbXi} {\widetilde{\bXi}}
\newcommand{\whbXi} {\widehat{\bXi}}
\newcommand{\bPi} {\boldsymbol{\Pi}}
\newcommand{\wtPi} {\widetilde{\Pi}}
\newcommand{\whPi} {\widehat{\Pi}}
\newcommand{\wtbPi} {\widetilde{\bPi}}
\newcommand{\whbPi} {\widehat{\bPi}}
\newcommand{\bSigma} {\boldsymbol{\Sigma}}
\newcommand{\wtSigma} {\widetilde{\Sigma}}
\newcommand{\whSigma} {\widehat{\Sigma}}
\newcommand{\wtbSigma} {\widetilde{\bSigma}}
\newcommand{\whbSigma} {\widehat{\bSigma}}
\newcommand{\bUpsilon} {\boldsymbol{\Upsilon}}
\newcommand{\wtUpsilon} {\widetilde{\Upsilon}}
\newcommand{\whUpsilon} {\widehat{\Upsilon}}
\newcommand{\wtbUpsilon}{\widetilde{\bUpsilon}}
\newcommand{\whbUpsilon}{\widehat{\bUpsilon}}
\newcommand{\bPhi} {\boldsymbol{\Phi}}
\newcommand{\wtPhi} {\widetilde{\Phi}}
\newcommand{\whPhi} {\widehat{\Phi}}
\newcommand{\wtbPhi} {\widetilde{\bPhi}}
\newcommand{\whbPhi} {\widehat{\bPhi}}
\newcommand{\bPsi} {\boldsymbol{\Psi}}
\newcommand{\wtPsi} {\widetilde{\Psi}}
\newcommand{\whPsi} {\widehat{\Psi}}
\newcommand{\wtbPsi} {\widetilde{\bPsi}}
\newcommand{\whbPsi} {\widehat{\bPsi}}
\newcommand{\bOmega} {\boldsymbol{\Omega}}
\newcommand{\wtOmega} {\widetilde{\Omega}}
\newcommand{\whOmega} {\widehat{\Omega}}
\newcommand{\wtbOmega} {\widetilde{\bOmega}}
\newcommand{\whbOmega} {\widehat{\bOmega}}
\newcommand{\bzero} {\mathbf{0}}
\newcommand{\bone} {\mathbf{1}}
\newcommand{\norm}[1]{\left\lVert #1 \right\rVert}
\newcommand{\abs}[1]{\left\lvert#1\right\rvert}
\newcommand{\ceil}[1]{\left \lceil #1 \right\rceil}
\newcommand{\argmin}{\operatorname*{arg\,min}}
\newcommand{\argmax}{\operatorname*{arg\,max}}
\)
One of the most famous algorithms in optimization and machine learning is “Gradient Descent.” It is a popular algorithm in the field of machine learning primarily because it is computationally efficient and easily scalable.
The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point because this is the direction of the steepest descent.
Learn More: Unraveling the Gradient Descent Algorithm: A Step-by -Step Guide
The stochastic gradient descent (SGD):
Like the gradient descent algorithm, SGD is also used to find the minimum of an objective function. The algorithm works by repeatedly taking steps in the direction of the negative gradient of the function, where the gradient measures the rate of change of the function at a given point. Now you may wonder if this has the same working principle as of the gradient descent algorithm. However, there is one subtle change in SGD: “It updates the solution by processing one data sample per algorithmic iteration “ .
Learn More: Mastering Stochastic Gradient Descent algorithm with the MNIST Dataset .
Main Difference:
SGD method process one data sample per algorithmic iteration and is used in one data arrives randomly hence the name stochastic .
GD method process all data samples or at least a batch of data samples in every algorithmic iteration.
In this article, we will compare the convergence comparison of gradient descent and stochastic gradient descent using regularized logistic regression as our loss function.
The Algorithms
Gradient Descent Method:
Algorithm 1 - Gradient Descent (GD)
Input: An arbitrary vector $\bx_0 \in \R^n$ and a decaying step size $\gamma_t > 0$;
1. for $t=1,2,\ldots,$ do
2. $\qquad$ Evaluate the gradient mapping at $\bx_t$, i.e., evaluate $\nabla f(\bx_t)$;
3. $\qquad$ Do the following update:
$\qquad$ $$ \bx_{t+1} := \bx_t - \gamma_t \nabla f(\bx_t) $$
4. end for
In above algorithm $\bx_t$ is the update of the objective variable $\bx$ at time $t$, $\nabla f(\bx_t)$ is the gradient of the loss function $f$.
Stochastic Gradient Descent:
Algorithm - Stochastic Gradient Descent (SGD)
Input: A random vector $\bx_0 \in \R^n$ and a decaying step size $\gamma_t > 0$;
1. for $t=1,2,\ldots,$ do
2. $\qquad$ Evaluate the stochastic gradient mapping at $\bx_t$, i.e., evaluate $\nabla F(\bx_t, \xi_t)$;
3. $\qquad$ Do the following update:
$\qquad$ $$ \bx_{t+1} := \cP_{\cX} \left(\bx_t - \gamma_t \nabla F(\bx_t, \xi_t) \right)$$
4. end for
In the above algorithm, $\bx_t$ is the update of the objective variable $\bx$ at time $t$, $\nabla f(\bx_t)$ is the gradient of the loss function $f$, and $\cP_{\cX}$ is the projection operator. We use the projection to ensure that the update of our algorithm doesn’t cause the objective variable $\bx$ to lie outside the feasible set, and if it does, the operator projects the update $\bx_{t+1}$ back to the feasible set. However, in this article, we will use the entire $\R^n$ as our feasible set, so we don’t need a projection operator.
Implementation
The core idea of this article is to test the performance of the SGD and GD algorithms on real-world data sets like MNIST and see the convergence behavior.
The Loss function – Regularized Logistic Regression
To test the convergence of the SGD vs GD algorithm on the MNIST dataset, we will use the regularized logistic regression loss function. MNIST data is a classification problem (we have a dataset of handwritten images, and we want to classify the digit of the handwritten image, hence the classification problem), so logistic regression is one of the famous machine learning techniques to solve the classification problem. The loss function is identified as follows:
$$
We will deal with one type of digit (say $3$), i.e., if the input is the image of digit $3$, we will identify the label as $1$, meaning correct, and $-1$ meaning incorrect. Say the input is of handwritten image $4$, then the corresponding label to this image is $-1$. This is why in the above loss function, we are denoting the label’s $v_i$ as a scalar quantity.
Remember, in stochastic gradient descent, we don’t have access to all $N_{train}$ data samples and in gradient descent we have access to entire training dataset $N_{train}$
So, we can compare the gradient descent and stochastic gradient update rule by taking the gradient of the above loss function as:
Gradient Descent Method: The update rule is given as follows:
$$
Stochastic Gradient Descent Method: We now use the index $j$ to fetch the random image and its label from the dataset. The update rule is given as follows:
$$
Python Code:
Import Libraries :
We need the ‘scikit-learn‘ library to download the MNIST dataset.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openmlDownload MNIST dataset :
mnist = fetch_openml('mnist_784', version=1)
mnist.keys()
U0, v0 = mnist["data"], mnist["target"]
U = U0.astype(np.double) # changes the attribute values to float
v = v0.astype(np.uint8) # changes labels from string to integerChange the labels:
Choose the image $3$ from the MNIST dataset and change its labels to
v_bin_3 = [2*int(v[i]==3)-1 for i in range(len(v))]Create a merged data frame of all samples with their corresponding labels :
U = np.array(U)
v = np.array(v_bin_3)
# Create df_data_merged using NumPy
df_data_merged = np.concatenate((U, v[:, None]), axis=1)Define a Split function:
The function below randomly chooses the $N_{train}$ samples from the entire dataset defined by the variable df_data_merged:
def split_train_and_convert(df_data_merged, train_set_size):
np.random.seed(0)
shuffled_indices = np.random.permutation(len(df_data_merged))
train_indices = shuffled_indices[:train_set_size]
train_set = df_data_merged[train_indices]
U_train = train_set[:, :-1]
v_train = train_set[:, -1:]
return U_train.T, v_train.TDefine the Loss function and gradient function :
Now we define the regularized logistic loss function and its gradient function for both Gradient Descent and Stochastic Gradient Descent methods:
## Define the given loss function (which is our regularized logistic loss regression
def loss_f(U_train,v_train,x,N_train):
output = 0
# The loss function is computed for all training images for each x
for i in range(N_train):
vU = np.dot(U_train[:, [i]],v_train[0, i])
vUx = vU.T@x
if (vUx > 709): # to avoid overflow, as python can't handle large numbers
output += vUx
else:
output += np.log(1 + np.exp(-vUx))
return output/N_train + (mu/2) * np.linalg.norm(x) ** 2
## Define the gradient of the objective function for gradient descent method
# we will process only one image
def grad_F(U_train,v_train,x):
d,N = np.shape(U_train) # d represents dimension of the data (image) which is 784
output = np.zeros((d, 1)) # initialize the output. gradient is a vector
for i in range(N_train):
vU = np.dot(U_train[:, [i]],v_train[0, i])
vUx = vU.T@x
# the min function is to avoid overflow, as python can't handle large numbers
output += (-vU / (1 + np.exp(min(709, vUx))))
return output/N_train + (mu * x)
## Define the gradient of the objective function for stochastic gradient descent method
def stoch_grad_F(U_train,v_train,x, i):
vU = np.dot(U_train[:, [i]],v_train[0, i])
vUx = vU.T@x
# the min function is to avoid overflow, as python can't handle large numbers
output = (mu * x) + ( -vU / (1 + np.exp(min(709, vUx))))
return outputDefine the Algorithm for “Stochastic Gradient Methods” and “Gradient Descent Methods”:
Now, we define the algorithm for the stochastic gradient algorithm and gradient algorithm; in both of the following functions, we will start with the initial point x_0 and evaluate the loss function at this point (in evaluation, we will use the entire training dataset of N_train samples). We use the concept of the epoch ; instead of evaluating the loss function at every update of the algorithm, we perform the update after a certain number of samples which we denote by epoch_length. The rest of the code has comments and is self-explanatory.
#%% Define the GD method
def GD(x_0, T_GD, stepsize, epoch_length, n_epoch, N_train,U_train,v_train):
f_epoch_vals = np.zeros(n_epoch+1)
# store the initial value of the objective function
f_epoch_vals[0] = loss_f(U_train,v_train,x_0,N_train).item()
x_next = x_0
c=1
for t in range(T_GD):
x_now = x_next
# No need to generate random sample in GD method
x_next = x_now - stepsize * grad_F(U_train,v_train,x_now)
## evaluate the loss function after every epoch_length iterations
if ((t + 1) % epoch_length) == 0:
f_epoch_vals[c] = loss_f(U_train,v_train,x_next,N_train).item()
c+=1
return f_epoch_vals
#%% Define the SGD method
def SGD(x_0, T_SGD, stepsize, epoch_length, n_epoch, N_train,U_train,v_train):
f_epoch_vals = np.zeros(n_epoch+1)
# store the initial value of the objective function
f_epoch_vals[0] = loss_f(U_train,v_train,x_0,N_train).item()
x_next = x_0
c=1
for t in range(T_SGD):
x_now = x_next
## generate random sample i (choose randomly any image)
rand_sample = np.random.randint(0, N_train)
x_next = x_now - stepsize * stoch_grad_F(U_train,v_train,x_now, rand_sample)
## evaluate the loss function after every epoch_length iterations
if ((t + 1) % epoch_length) == 0:
f_epoch_vals[c] = loss_f(U_train,v_train,x_next,N_train).item()
c+=1
return f_epoch_vals
Initial Parameters :
We have finished the main functions, and now we move to the defining parameters of the code (like stepsize, initial start point, number of training samples $N_{train}$ etc. for both algorithms) so we can call the functions defined above:
## Generate train and test data
N_train = 63000
U_train, v_train = split_train_and_convert(df_data_merged, N_train)
d = U_train.shape[0] # dimension of the data
x_0 = np.zeros((d, 1)) # initial start point
stepsize = 10 ** -6
n_epoch = 10 # It denotes the number of evaluated points in the objective function plot
T_SGD = int(N_train*n_epoch) # Total number of iterations for Stochastic Gradient Descent (SGD) method
T_GD = int(n_epoch) # Total number of iterations for Gradient Descent (GD) method
epoch_length_SGD = int(T_SGD/n_epoch) # Number of iterations per epoch
epoch_length_GD = int(1) # Number of iterations per epoch
mu = 10 ** -2 # regularizing parameter of loss functionCall the Algorithms :
Now we execute the algorithms and store the evaluated values of the loss functions:
# run SGD
f_epoch_SGD = SGD(x_0, T_SGD, stepsize, epoch_length_SGD, n_epoch, N_train,U_train,v_train)
# run GD
f_epoch_GD = GD(x_0, T_GD, stepsize, epoch_length_GD, n_epoch, N_train,U_train,v_train)Plot the final result:
fig = plt.figure(figsize=(12,8))
plt.plot(range(0,len(f_epoch_SGD)),f_epoch_SGD,color='blue',
marker='*',markersize=10,linestyle='solid',label="SGD convergence | BraveLearn",linewidth=4)
plt.plot(range(0,len(f_epoch_GD)),f_epoch_GD,color='red',
marker='+',markersize=10,linestyle='solid',label="GD convergence | BraveLearn",linewidth=4)
plt.legend(loc=1,fontsize=12)
plt.xlabel('Number of iterations (t)', color='#1C2833',fontsize=12)
plt.ylabel(r"$\left(\frac{1}{N_{train}}\sum_{i \in N_{train}} \ln(1+exp(-v_i \mathbf{u_i^T x_t} \right)+\frac{\mu}{2}\||x_t\||^2$", color='#1C2833',fontsize=18)
plt.grid(True)
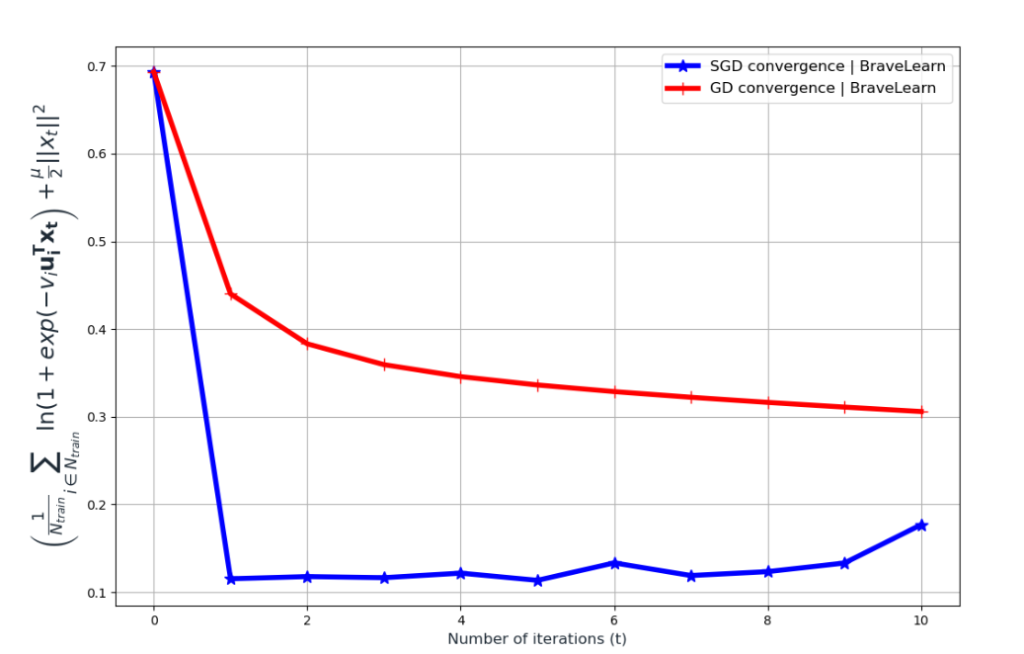
plt.show()The Plot:
Enjoy implementing the stochastic gradient descent and gradient descent algorithms on the MNIST dataset and do experiments with the different step sizes to observe their performance impact on convergence.
Thought of the article: Why SGD has better performance then GD?
Leave your answers in the comments.