Half Adder and Full Adder using Hierarchical Designing in Verilog

This tutorial focuses on writing Verilog code in a hierarchical style. In “Introduction to Verilog” we have mentioned that it is a good practice to write modules for each block. This tutorial will further provide some examples and explain why it is better to code in a hierarchical style.

Hierarchical Designing: A Hierarchical methodology is used to design simple components to construct more complex component. The key idea is to divide and conquer i.e. to divide the big complex circuit into smaller modules and further dividing these modules to even smaller modules like gates etc.

There are two design approaches when writing code in hierarchical style

Top-Down Methodology
Bottom-Up Methodology

Top-Down Methodology: In Top-Down we first identify or define the big circuit or big block and then identify a small block used to make this big block. We further divide the small block to leaf cells which cannot be further divided. e.g. you want to construct full adder, so you immediately identify two small blocks i.e. half adder.

Bottom-Up Methodology: In this approach, we first identify small blocks that are available to us and use them to construct a big block. E.g., you have two half adders available, and you can construct a full adder using these two half adders.

Typically designers use these two approaches side-by-side to construct complex circuits. Design architects define the specifications of the top-level block. Logic designers decide how the design should be structured by breaking up the functionality into blocks and sub-blocks. At the same time, circuit designers are designing optimized circuits for leaf-level cells. They build higher-level cells by using these leaf cells.

Instance: Before proceeding towards examples, we would like to clarify the concept of “instance”. An instance is a copy of a module created when a big component calls a smaller component. An instance must have a unique name. The following examples will help you clarify the concept of instantiation and hierarchical designing.

Example-1: Design and simulate Half-Adder using gate-level modelling.

Truth Table: Given below is the truth table for half adder:

Input		Output
A	B	Sum	Carry
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

From the above table of Half adder we can construct its boolean expression given below:

[latex]\text{ Sum } = A’B + AB’ = A \text{ XOR } B [/latex]

[latex]\text{ Carry } = AB = A \text{ AND } B[/latex]

Hence gate-level diagram constructed as:

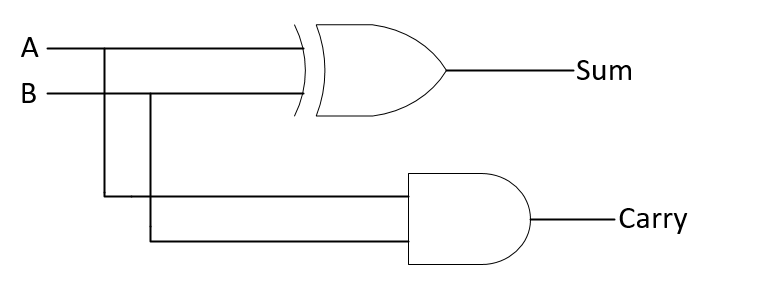
Verilog Code:


module half_adder(sum, carry, a, b); 
input a, b; 
output sum, carry; 
xor sum1(sum, a, b); 
and carry1(carry, a, b); 
endmodule

TestBench Code:


`timescale 1ns / 1ns 
module half_adder_tb; 
wire t_sum, t_carry; 
reg t_a, t_b; 
half_adder my_design(.a(t_a), .b(t_b), .sum(t_sum), .carry(t_carry)); 
initial 
begin // 1 
t_a = 1'b0;
t_b = 1'b0;
#5 //2 
t_a = 1'b0; 
t_b = 1'b1;
#5 //3 
t_a = 1'b1; 
t_b = 1'b0;
#5 //4 
t_a = 1'b1; 
t_b = 1'b1;
end 
endmodule

The above code is written for half adder you may see no hierarchical style coding in it as half adder cannot be further divided but we can construct full adder by using two half adder which is shown below as well. But first lets see its simulated waveform:

Simulated Waveform of Half Adder

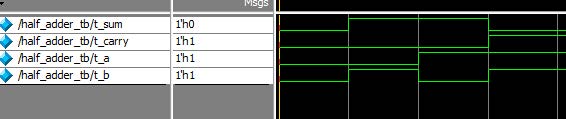
By comparing the truth table and above waveform we can clearly observe that half adder works properly.

Now lets design Full Adder by using two Half Adders.

Example-2: Design a full adder by using two half adder.

Truth table is given below:

Input			Output
A	B	Carry In	Sum	Carry
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

By observing truth table for full adder we can deduce its output boolean expression given below:

[latex]\begin{align*}\text{ Sum } =& A’B’C + A’BC’+ AB’C’ + ABC \\=& A'(B’C + BC’) + A(B’C’ + BC) = A(B \oplus C) + A’ ( \overline{B \oplus C} ) \\ =& A \oplus B \oplus C \end{align*}[/latex]

[latex]\begin{align*} \text{ Carry } =& A’BC + AB’C + ABC’ + ABC \\ =& C(A’B + AB’) + AB (C’+C) \\ =& C(A \oplus B) + AB \end{align*}[/latex]

As we can clearly see from boolean expressions that full adder can be constructed by using two half adders. A block diagram for this is shown below:

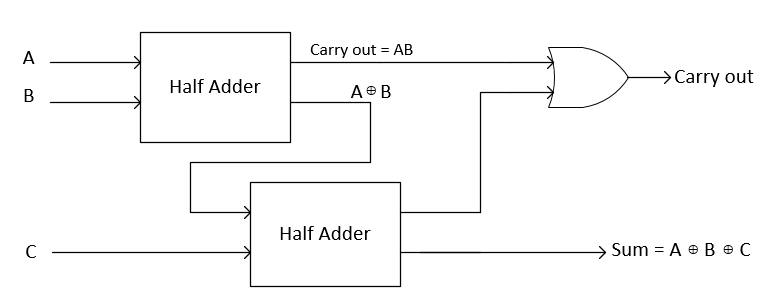
By using hierarchical style coding we can construct full adder using two half adder as shown in the block diagram above

Verilog Code:


module full_adder_join(fsum, fcarry_out, a, b, c); 
input a, b, c; 
output fsum, fcarry_out; 
wire half_sum_1, half_carry_1, half_carry_2; 
half_adder HA1(half_sum_1, half_carry_1, a, b); //instance 1 of Half Adder
half_adder HA2(fsum, half_carry_2, half_sum_1, c); //instance 2 of Half Adder
or or1(fcarry_out, half_carry_2, half_carry_1); 
endmodule

where half adders code are already mentioned in Example-1. Note that we have called half adder 2 times as shown in block diagram as well. This will create two instance of the same module.

Test Bench Code:


`timescale 1ns / 1ns 
module full_adder_2_HA_tb; 
wire t_out_sum, t_out_carry; 
reg t_a, t_b, t_c; 
full_adder_join my_full_adder(.a(t_a), .b(t_b), .c(t_c), .fsum(t_out_sum), .fcarry_out(t_out_carry)); 
initial 
begin // 1 
t_a = 1'b0; 
t_b = 1'b0; 
t_c = 1'b0;
#5 //2 
t_a = 1'b0; 
t_b = 1'b0; 
t_c = 1'b1;
#5 //3 
t_a = 1'b0; 
t_b = 1'b1; 
t_c = 1'b0;
#5 //4 
t_a = 1'b0; 
t_b = 1'b1; 
t_c = 1'b1;
#5 //5 
t_a = 1'b1; 
t_b = 1'b0; 
t_c = 1'b0;
#5 //6 
t_a = 1'b1; 
t_b = 1'b0; 
t_c = 1'b1;
#5 //7 
t_a = 1'b1; 
t_b = 1'b1; 
t_c = 1'b0;
#5 //8
t_a = 1'b1; 
t_b = 1'b1; 
t_c = 1'b1;
end 
endmodule

The above code is simulated in Modelsim and below are the simulated result: