Earlier we discussed the introduction of a continuous random variable and cumulative distribution function. Please see this article if you haven’t read it about already.
Now we will give some problems related to Cumulative distribution function so you can have a deeper understanding of this topic. These problems are adapted from the following textbook:
“Probability and Random Processes by Scott Miller 2nd Edition.”
Problem-1: Which of the following mathematical functions could be the CDF of some random variable?
Remember: To be a CDF of some random variable, the function [latex]F_{X}(x)[/latex] must start at zero when [latex]x = -\infty[/latex], end at one when [latex]x = \infty[/latex], and be monotonic increasing in between
[latex] 1- \begin{eqnarray*} F_X(x) &=& 1-|x|, & |x| \leq 1,\\ & & 0 , & |x| <1 \end{eqnarray*} [/latex]
Answer: This cannot be the CDF of a random variable since the function is not monotonic increasing
[latex] 2- \begin{eqnarray*} F_X(x) &=& \frac{1}{2} e^x, & x < 0,\\ & & 1 – \frac{1}{2} e^{-x} , & x \geq 0 \end{eqnarray*} [/latex]
Answer: [latex]F_{X}(x)[/latex] satisfies the necessary conditions, and thus could be the CDF of some random variable.
[latex] 3- \begin{eqnarray*} F_X(x) &=& 0, & x \leq 0,\\ & & x^2 , & 0 < x \leq 1 \\ & & 1 , & x > 1 \end{eqnarray*} [/latex]
Answer: [latex]F_{X}(x)[/latex] satisfies the necessary conditions, and thus could be the CDF of some random variable
[latex] 4- F_X(x) = log(x)u(x)[/latex]
Answer: This function cannot be the CDF of some random function. Taking the limit as [latex]x \rightarrow \infty[/latex] we see the function will grow without bound, so it will not end at one as required.
Problem-2: Suppose a random variable has a CDF given by:
[latex]\begin{equation*} F_X(x) = \frac{x^2}{1+x^2} u(x) \end{equation*}[/latex]
Find the following quantities:
(a) [latex]Pr(X<2)[/latex]
(b) [latex]Pr(X>4)[/latex]
(c) [latex]Pr(1 < X < 3)[/latex]
(d) [latex]Pr(X>2 | X < 4)[/latex]
Solution: (a) [latex]Pr(X<2) = F_{x}(2) = \frac{2^{2}}{1+2^{2}} = 4/5[/latex]
(b) [latex]Pr(X>4) = 1-Pr(X\leq4) = 1 – F_{x}(4) = 1 – \frac{4^{2}}{1+4^{2}} = 1/17[/latex]
(c) [latex]Pr(1<X<3) = Pr(X<3) – Pr(X<1) = Pr(X<3) – Pr(X<1) = F_{x}(3) – F_{x}(1) \\
= \frac{3^{2}}{1+3^{2}} – \frac{1^{2}}{1+1^{2}} = 2/5[/latex]
(d) [latex]Pr(X>2 | X<4) = {\displaystyle \frac{\text{Pr}\bigg((X>2)\cap(X<4)\bigg)}{\text{Pr}(X<4)} \\
=\frac{\text{Pr}(2<X<4)}{\text{Pr}(X<4)}=\frac{F_{x}(4)-F_{x}(2)}{F_{x}(4)}} \\
= {\displaystyle {\frac{\frac{4^{2}}{1+4^{2}}-\frac{2^{2}}{1+2^{2}}}{\frac{4^{2}}{1+4^{2}}}}} \\
= 3/20 = 0.15[/latex]
Problem-3: Now Suppose a random variable has a CDF given by:
[latex]\begin{equation*} F_X(x) = \left( \frac{1}{2} + \frac{1}{\pi} tan^{-1}(x) \right) u(x)\end{equation*}[/latex]
Find the following quantities:
(a) [latex]Pr(X<2)[/latex]
(b) [latex]Pr(X>4)[/latex]
(c) [latex]Pr(1 < X < 3)[/latex]
(d) [latex]Pr(X>2 | X < 4)[/latex]
Solution: (a) [latex]Pr(X<2) = F_{x}(2) = \big(\frac{1}{2} + \frac{1}{\pi} tan^{-1}(2) \big). \\[/latex]
(b) [latex]Pr(X>4) = 1-Pr(X \leq 4) = 1 – F_{x}(4) \\
= 1 – \big(\frac{1}{2} + \frac{1}{\pi} tan^{-1}(4) \big) \\
= \big(\frac{1}{2} – \frac{1}{\pi} tan$^{-1}(4) \big). \\[/latex]
(c) [latex]Pr(1<X<3) = Pr(X<3) – Pr(X<1) = F_{x}(3) – F_{x}(1) \\
= \big(\frac{1}{2} + \frac{1}{\pi} tan^{-1}(3) \big) -\big(\frac{1}{2} + \frac{1}{\pi} tan^{-1}(1) \big) \\
= \frac{1}{\pi} tan^{-1}(3) – \frac{1}{\pi} tan^{-1}(1) \\[/latex]
Since [latex]tan^{-1}(1) = \frac{\pi}{4}[/latex], we have
[latex]Pr(1<X<3)=-\frac{1}{4}+\frac{1}{\pi}\tan^{-1}(3). \\[/latex]
(d) [latex]Pr(X>2 | X<4)[/latex]
[latex]\begin{align*}
{\displaystyle } & =\frac{\text{Pr}\bigg((X>2)\cap(X<4)\bigg)}{\text{Pr}(X<4)}=\frac{\text{Pr}(2<X<4)}{\text{Pr}(X<4)}=\frac{F_{x}(4)-F_{x}(2)}{F_{x}(4)}\\
& =\frac{\big(\frac{1}{2}+\frac{1}{\pi}\tan^{-1}(4)\big)-\big(\frac{1}{2}+\frac{1}{\pi}\tan^{-1}(2)\big)}{\big(\frac{1}{2}+\frac{1}{\pi}\tan^{-1}(4)\big)}=\frac{\tan^{-1}(4)-\tan^{-1}(2)}{\frac{\pi}{2}+\tan^{-1}(4)}.
\end{align*}[/latex]
Problem-3: Suppose we flip a balanced coin five times and let the random variable [latex]X[/latex] represent the
number of times heads occurs.
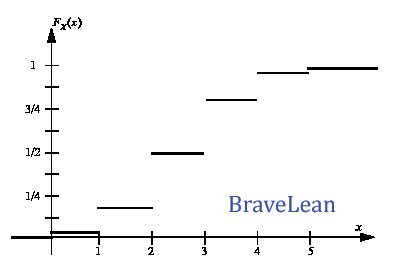
(a) Sketch the CDF of [latex]X, F_X(x)[/latex]
(b) Write [latex]F_X(x)[/latex] analytically in terms of unit step functions.
Solution: (a) Let X be the number of heads in five coin tosses, so X can be 0, 1, 2, 3, 4, or 5.
[latex]Pr(X=0) = (\frac{1}{2})^{5} = \frac{1}{32}. \\
Pr(X=1) = {5 \choose 1}\big(\frac{1}{2}\big)^{4}\big(\frac{1}{2}\big)^{1} = \frac{5}{32}. \\
Pr(X=2) = {5 \choose 2}\big(\frac{1}{2}\big)^{3}\big(\frac{1}{2}\big)^{2} = \frac{10}{32}. \\
Pr(X=3) = {5 \choose 3}\big(\frac{1}{2}\big)^{2}\big(\frac{1}{2}\big)^{3} = \frac{10}{32}. \\
Pr(X=4) = {5 \choose 4}\big(\frac{1}{2}\big)^{4}\big(\frac{1}{2}\big)^{1} = \frac{5}{32}. \\
Pr(X=5) = {5 \choose 5}\big(\frac{1}{2}\big)^{5} = \frac{1}{32}. \\[/latex]
Now [latex]F_{x}(x) = {\displaystyle {\sum_{i=1}^{k}}} P_{x}(x_{i}), for x_{k}\leq x \leq x_{k+1} \\[/latex]
[latex]
F_{x}(x)=\left\{ \begin{array}{ll}
0 & \quad\text{for x < 0}\\
1/32 & \quad\text{for 0 \leq x < 1}\\
6/32 & \quad\text{for 1 \leq x < 2}\\
1/2 & \quad\text{for 2 \leq x < 3}\\
26/32 & \quad\text{for 3 \leq x < 4}\\
31/32 & \quad\text{for 4 \leq x < 5}\\
1 & \quad\text{for 5 \leq x}
\end{array}\right.
[/latex]
(b) [latex]F_{x}(x) = \frac{1}{32}u(t) + \frac{5}{32}u(t-1) + \frac{10}{32}u(t-2) + \frac{10}{32}u(t-3) + \frac{5}{32}u(t-4) + \frac{1}{32}u(t-5)[/latex]